Statistics Without Borders Helps UNICEF
Stephanie Eckman, Monica Dashen, Aliou Diouf Mballo, and Robert Johnston
It is important when working with GPS data to pay attention to the precision with which each coordinate is collected, usually expressed as the radius of the 68% confidence interval around the coordinate. Precision is affected by several factors, including how many satellites the device has located and interference from nearby objects.
Data collection on mobile devices opens the possibility of collecting global positioning system (GPS) coordinates, time stamps, and other forms of paradata during survey interviews, often at very low cost, and these data are increasingly used to perform real-time quality checks on collected survey data. Robert Johnston (of UNICEF) contacted Statistics without Borders (SWB) for support in analyzing the time stamps and GPS points collected during UNICEF’s nutrition surveys to validate the surveys’ sample selection techniques.
The UNICEF nutrition surveys have been conducted in West and Central Africa since 2005 and have recently transitioned to tablet computers, which allow for more paradata collection. (Paradata are data collected as a byproduct of survey data collection; see Improving Surveys with Paradata: Analytic Uses of Process Information for more information). When a frame or sample of households from alternative sources is not available (or affordable), the team of three interviewers selects a systematic sample of households in each cluster using list-and-go, giving each household the same probability of selection. At each selected household, interviewers record the height and weight of children under the age of five, as well as other household and person-level data.
Johnston’s concern was the possibility of bias in the survey data if interviewers were not following the sample selection protocol. Traditional methods to detect deviations in selection involve frequency distributions to identify clusters of outliers and route verification by supervisors; UNICEF already has integrated these procedures into an online dashboard. UNICEF-SWB sought to add to this toolkit using GPS coordinates and time stamp paradata captured by the survey instrument. UNICEF provided data from a 2014 national survey. More than 27,000 GPS coordinates of interviewed households lit up our maps, indicating interviews were conducted throughout the country. Zooming into the rural areas, about 20 points appeared in each village. Connecting the GPS coordinates to household number revealed the interviewers’ route—from the first to the last household visited.
Unfortunately, georeferenced cluster maps were not freely available, as is common in developing countries, which made review of the sample difficult. We did not know, for instance, if the sampled points fell in the right cluster, or if the interviewers had included households outside the selected cluster. Furthermore, we could not tell if the interviewers had walked throughout the entire cluster, as called for in the directions, or if they simply picked the first households they came upon.
Faced with a large data set of GPS coordinates and no appropriate georeferenced map, SWB volunteers devised three tests involving GPS coordinates and time stamps to detect unexpected variation. The first involved testing the distance between GPS points, that is, whether interviewers seemed to have stood in one place while collecting data, suggesting a convenience rather than a random sample, or moved throughout the cluster. We calculated the distance between consecutive sampled housing units in each cluster. Only 1.7% of these distances were less than five feet; the mean distance was 181 ft. The average distance interviewers walked was lower in the two urban states (166.33 ft.) than in the rural states (181.35 ft.), which makes sense—urban areas are more densely populated than rural. These findings suggested that the interviewers walked around the intended area and did not expedite data collection by reducing the area covered. A recent Washington Statistical Society presentation by Aref Dajani and Rodrick Marquette used a similar test in the U.S. to detect falsification. We also tried repeating this analysis with time stamps, calculating the time between consecutive housing units, but the time stamp data were harder to work with, as interviewers often had more than one case open at a time and returned to households they had partially completed earlier.
The second test involved using time stamps to detect response fabrication, rather than convenience sampling. Incredibly short interview durations might suggest curb stoning. However, the results indicated that interview time increased with the number of people in a household, as expected. We also found that a small number of time stamps were fairly long, most likely because interviewers could not tell whether they closed out a case until the end of the day, which points to instrument usability issues.
The third test compared the area covered by the interviewers to a measure of cluster size: Everything else being equal, the interviews should be more widely dispersed in high-population clusters and less so in small clusters. As a proxy for cluster size, we could use the number of households in the cluster, which is collected during the sampling stage or available from census data. As a measure of the area covered by interviewers in a given cluster, we could use any of a number of measures: the total distance between interviewed households; the area of the smallest rectangle enclosing the selected points; the convex hull of the selected points.
Plotting the cluster size and the area covered against each other, we should see a positive slope: any teams, which are consistent outliers, especially in the negative direction (a small area covered in clusters with large population), should be flagged for more follow up. Figure 1 shows such a graph. It identifies two clusters with about 200 housing units worked by Team 21 that have low areas in large clusters. Note, however, that Team 21 also has two clusters near the top of the graph, that is, with high areas.
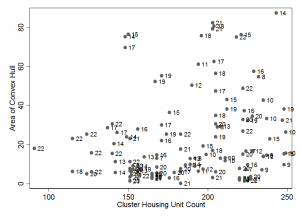
Figure 1: Relationship between Cluster Housing Unit Count and Sample Dispersion; labels refer to interviewer teams. Teams that are outliers near the bottom of the graph may not have covered all housing units in their assigned clusters.
A more formal implementation of this test involves building a model in which the dependent variable is one of the measures of the area covered by the sampled points and the independent variables are cluster characteristics such as household count, population, urban/rural, and state. The model should also have random intercepts for each interviewing team, as well as random slopes on the cluster size variable. Teams that are statistical outliers in terms of the random effects, that is, those with low empirical best linear unbiased predictors (EBLUPs), would then be flagged for closer inspection. A similar approach is used to detect underperforming interviewers in an article by Brady West and Robert Groves from 2013, titled “The PAIP Score: A Propensity-Adjusted Interviewer Performance Indicator.” Sample code for calculating convex hulls from GPS coordinates in Python and for fitting random effects models and predicting EBLUPs in Stata is given on github.
In developing countries, the use of GPS coordinates to detect substitutions is difficult, as georeferenced maps are not always available. The SWB team on this project developed three tests that could be used to review the quality of interviewer-selected samples in such situations. We hope that these tests, combined with the more traditional methods of falsification and substitution detection, prove useful to researchers who would like to use real-time techniques to ensure the quality of interviewer-selected samples.
Learn more about Statistics without Borders’ other projects and get involved.

















