Statistics and the Human Element

Barry D. Nussbaum
For years, I have given seminars on statistical communications. Readers of this column will realize I use my mantra, “It’s not what we said, it’s not what they heard, it’s what they say they heard,” over and over again. All this is aimed at how we present results and conclusions after some statistical analysis. This month, I reflect a bit on the human element that goes into analytical work before the first equation is even applied.
The Unconscious Bayesian
I am well aware of the “law of the unconscious statistician,” which concerns itself with taking the mean of a function of a random variable. I don’t really consider myself a Bayesian (not a frequentist, either), yet I wonder how much we are unconsciously Bayesian in nature just by evaluating the situation based on our prior knowledge of life events.
This came to my attention many years ago, when our family was returning from Miami to Washington. Based on ticket prices, the thrifty one of us (who eventually became ASA president) purchased return tickets for December 31, instead of January 1. This upset my late wife who realized we would miss seeing the Orange Bowl parade in person. There had been awful weather in Washington and many cancelled flights on prior days, so my family found ourselves in five seats widely scattered on a packed aircraft. The attendant made some announcement about needing five volunteers to step off. Before she finished the announcement, I heard a familiar voice from two rows behind me say, “Hey, dad, mom just gave away our seats.” Sure enough, there was Debbie waving in the front of the plane for us to all get off.
I tried to calculate in my head the probability of getting five seats on another flight. This subjective probability decreased substantially as a man said to me what a dumb move this was since his family had waited through three days of canceled flights just to get on this one. I guess this was Bayesian in nature. What I missed was Debbie charming the gate agent—in Spanish no less—into giving us five first-class seats on a flight the next day. Hmmm, the human element at work. Off to the parade we went, and the kids still made it back to school.
Too Many Variables
Discomfort Index: When I was a boy, a typical summer weather report included the “discomfort” index. Oh, we knew the temperature and humidity joined together to make it miserable, but now we had a quantitative measure. Eventually, political correctness set in and it became either the temperature-humidity index or the heat index.
Jo Craven McGinty of The Wall Street Journal, who was my invited speaker at the recent JSM, wrote a wonderful column describing how this is calculated (July 7, 2017). There is a nine-term regression equation used to calculate the heat index. My favorite term involves the independent variable T*T*RH*RH, which is the square of the product of temperature and relative humidity.
Did anybody wonder what the units of this term must be? Perhaps degrees squared percentage squared? What does that mean? The coefficient of this term in the heat index equation is a mind numbing 0.00000199. (I can still envision Mrs. Chenofsky’s middle-school lecture about significant digits.) Are they really serious about the term 0.00000199 T*T*RH*RH? If that isn’t bad enough, this only pertains to a 5-foot-7-inch person weighing 147 pounds and a few other restrictions. Great. Now I am too short and too heavy to be uncomfortable. That hardly makes me comfortable. Did some human really do this? Must have been a government committee.
Too Few Variables
A Royal Pain: During JSM, the Kansas City Royals were playing the Baltimore Orioles in Camden Yards, just steps from the convention center. What makes the Royals different from other major league teams? Apparently, PERCOTA, the fancy computer model for predicting major league baseball success is quite accurate. The Wall Street Journal’s Jared Diamond (August 16, 2017) reported PERCOTA correctly predicted total games won within 3.25 games for two-thirds of the teams from 2013 on.
But, it is always wrong for the Kansas City Royals. From 2013 to 2016, they were winning an average of 12.5 games more than PERCOTA predicted. (By the way, PERCOTA was originally developed by Nate Silver and stands for “player empirical comparison and optimization test algorithm.” Yeah, just what you thought it stood for!)
Now it seems to me PERCOTA works pretty well. The fact that the Royals do better than anticipated makes the game fun and probably represents what we statisticians know about random chance. But the humans who run PERCOTA seem destined to fine tune it. They just can’t allow the Royals to be more efficient at winning games than they predicted. If they ever get PERCOTA perfected, we can stop attending the games. That doesn’t sound like much fun.
Who Picked Those Lines?
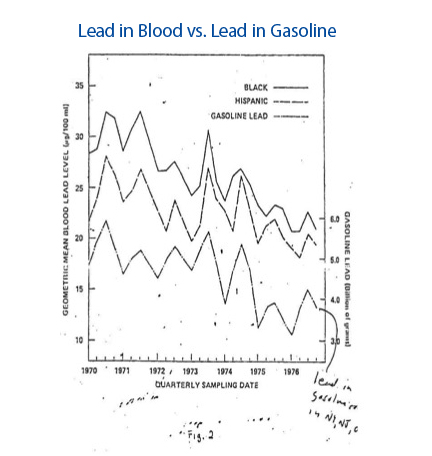
In my seminars about statistical communications, I always include a fairly simple graph depicting the correlation between the amount of elemental lead in gasoline (when gasoline still contained tetraethyl lead) with the blood lead levels of both black children and Hispanic children.
The back story here is that the country was trying to avoid long gas lines as had occurred during the Arab oil embargo of 1973. While correlation certainly does not imply causation, all the other usual suspects—such as children eating paint chips—could not explain the pronounced seasonal correlation shown in the graph.
The graph landed on the desk of President Jimmy Carter, and he used it in his decision to permit the US Environmental Protection Agency to proceed with its program to phase lead out of gasoline. He stated he did not want any policy that might have a particularly deleterious effect on these two groups.
Frequently, I am asked why there is no line showing the blood lead levels of white children. The easy answer is that the white line would have the same seasonal and decreasing trends as the other two groups, but at a lower absolute level. But, the primitive plotting equipment we had at the time made it difficult to add another line. However, I have always thought the more interesting question is what if there were only one line showing blood lead levels as a whole, without showing separate lines by race. There would be the same trend and seasonality, but would the president’s decision have been the same?
With the benefit of hindsight, Carter was concerned about the harmful effects on minority populations. Would he have even have known this if the graph just had one composite line for blood lead?
So here again, the human element may well have set the course of a presidential decision. And, for me, this is particularly intriguing since the human involved was me. Did I unwittingly or unknowingly really affect a major policy direction by simply selecting certain variables to put on the graph?
While I think the decision was the right one from a national policy point of view (of course, this is hardly an unbiased view after a 40-year career with EPA), it is a haunting feeling that the fairly novice analyst I was back in those day could have really had such a hand in a presidential directive.
With apologies to Pogo, we have met the human and he is me.
Significantly forward,
Barry










[…] last week, reader David P. pointed me to a column by Barry Nussbaum, chief statistician at the EPA for over a decade and currently president of the American Statistical […]
[…] last week, reader David P. pointed me to a column by Barry Nussbaum, chief statistician at the EPA for over a decade and currently president of the American […]
Blogging Areas
Statistics and the Human Element | Amstat News
Welcome!
Amstat News is the monthly membership magazine of the American Statistical Association, bringing you news and notices of the ASA, its chapters, its sections, and its members. Other departments in the magazine include announcements and news of upcoming meetings, continuing education courses, and statistics awards.
ASA HOME
Departments
Archives
ADVERTISERS
PROFESSIONAL OPPORTUNITIES
FDA
US Census Bureau
Software
STATA
QUOTABLE
“ My ASA friendships and partnerships are some of my most treasured, especially because the ASA has enabled me to work across many institutional boundaries and
with colleagues from many types of organizations.”
— Mark Daniel Ward
Editorial Staff
Managing Editor
Megan Murphy
Graphic Designers / Production Coordinators
Olivia Brown
Meg Ruyle
Communications Strategist
Val Nirala
Advertising Manager
Christina Bonner
Contributing Staff Members
Kim Gilliam
Contact us
Amstat News
American Statistical Association
732 North Washington Street
Alexandria, VA 22314-1904
(703) 684-1221
www.amstat.org
Address Changes
Amstat News Advertising