Stochastic Search Model Featured in August Issue
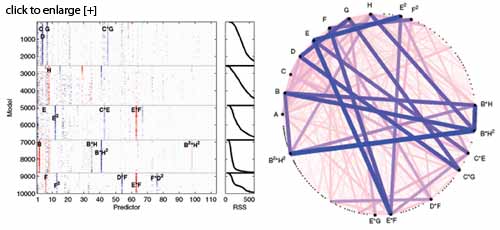
Simultaneous display of coefficients (columns) in 10,000 models (rows). Darkness indicates coefficient size, and zero coefficients are white. Color indicates coefficient sign. Right: link plot, with bold lines indicating co-occurrence of pairs of variables in good models.
Screening experiments based on nonregular designs present both promise and peril. Their complex aliasing structure opens a plethora of possible subsets of important effects, while at the same time providing scant information for discriminating between subsets. In the paper “Simulated Annealing Model Search for Subset Selection in Screening Experiments,” Mark A. Wolters and Derek Bingham invent an effective algorithm for the regression model selection problem having a large number of predictors and only a few trials. The problem is further compounded by the desire to identify possibly active interactions, while obeying “heredity” constraints, such as the inclusion of a two-factor interaction requiring the inclusion of two corresponding main effects.
Common subset selection methods do not perform well in this setting. The method uses an intentionally nonconvergent stochastic search to generate a large set of well-fitting models, each with the same number of variables. Model selection is then viewed as a feature extraction problem from this set. An easy-to-use graphical method, involving plots such as the above to detect interactions and sift through promising subsets, is proposed, along with an automatic approach to determine the best models. This paper will be presented in the Technometrics session at the Fall Technical Conference in October.
Although regression problems typically focus on the estimation of a response function, we are sometimes more interested in its derivative. Richard Charnigo, Benjamin Hall, and Cidambi Srinivasan tackle this problem in their paper, “A Generalized Cp Criterion for Derivative Estimation,” which focuses on effective selection of a tuning parameter in nonparametric regression. The paper provides both empirical support for the new GCp criterion through simulation studies and theoretical justification in the form of an asymptotic efficiency result. A motivating practical application in analytic chemistry illustrates the approach and demonstrates the capabilities of the selection criterion.
Gaussian process models have become a ubiquitous approach to approximating deterministic computer experiments, but they can have problems with computational complexity and numerical instability. In the paper “Regression-Based Inverse Distance Weighting with Applications to Computer Experiments,” V. Roshan Joseph and Lulu Kang challenge the dominance of Gaussian processes. They demonstrate that by combining inverse distance weighting with linear regression, a simple, flexible, computationally efficient, and accurate method for multivariate interpolation is obtained. The method works well in high dimensions and with large data sets. This paper was presented in the Technometrics session at JSM this month.
In “A Simple Approach to Emulation for Computer Models with Qualitative and Quantitative Factors,” Qiang Zhou, Peter Z. G. Qian, and Shiyu Zhou propose a flexible, yet computationally efficient, approach for building Gaussian process models for computer experiments with mixed input types. By using a novel hypersphere parameterization to model the correlations of the qualitative factors, the paper eliminates constraints from associated optimization problems. Several examples illustrate the effectiveness and computational efficiency of the proposed approach.
Foldover is a widely used procedure for selecting follow-up experimental runs. Foldover designs can, however, be inefficient, requiring twice as many runs as the initial design. Semifolding, in which half a foldover fraction is added, is investigated in “Optimal Semifoldover Plans for Two-Level Orthogonal Designs,” by David J. Edwards. The paper develops optimal plans for two-level orthogonal factorial designs (regular and nonregular) and makes comparisons based on the concept of minimal dependent sets. A hidden projection property of optimal semifoldovers of 12- and 20-run orthogonal arrays is uncovered.
The explosion of sparse regularization methods in regression is having significant effects in other statistical problems. The next two papers both explore sparse methods in the context of multivariate statistical process control, especially with complex data structures such as profile and multistage process monitoring. First, Giovanna Capizzi and Guido Masarotto demonstrate convincingly in the paper “A Least-Angle Regression Control Chart for Multidimensional Data” that out-of-control conditions can be detected with superior efficiency when a limited subset of variables is considered. The second paper, “A LASSO-Based Diagnostic Framework for Multivariate Statistical Process Control” by Changliang Zou, Wei Jiang, and Fugee Tsung, focuses on accurate fault diagnosis of responsible factors. Such diagnosis has become increasingly critical in a variety of applications that involve rich process data. The LASSO algorithm allows quick computation of the diagnostic result, comparable with a least-squares regression.
The issue closes with “Spatially Varying Autoregressive Processes” by Aline A. Nobre, Bruno Sansó, and Alexandra M. Schmidt. This paper considers models for processes exhibiting correlation in both time and space, based on autoregressive processes at each location. Through the analysis of satellite data on sea surface temperature for the North Pacific, the paper illustrates how the model can be used to separate trends, cycles, and short-term variability for high-frequency environmental data.