Daniel Smith has been a reliability engineer at Cox Communications since 2005. He completed his undergraduate studies at Emory University and earned an MBA with a concentration in statistics at the Georgia Institute of Technology, where he also received his Six Sigma Black Belt training.

First published in 1960, Theodore Levitt wrote an inspiring article, titled “Marketing Myopia.” The general sense of the article noted that many companies were incorrectly branding themselves into a narrow corner of their respective marketplace, whereas they could have been able to grow exponentially if only they had a broader sense of meeting customer needs. Examples in the paper included how the railroad industry saw itself in a niche market rather than the broader industry of transportation. There were also success stories captured, such as oil companies who viewed themselves in the sector of energy, rather than petroleum.

A similar phenomenon is occurring in the management philosophy known as Six Sigma. When Motorola first branded this concept in the 1980s, it seemed to take off like a rocket. Early adopters praised the concept as revolutionary for many reasons. Executives in the upper management levels of corporations seemed to like the step-by-step structure given to projects following this idea of reducing defects through advanced analytics, and employees were happy to receive accreditation/certification for their professional careers. Win-win, right? Well, not so fast.

While practitioners who correctly apply the ideas and tenets set forth in Six Sigma training certainly wreak massive benefits for the companies they work for, there are also a plethora of employees who incorrectly apply many concepts, and often these employees don’t have anyone overseeing their work to know these mistakes are being made. While there are countless examples of this occurring in businesses across the world, the three listed below are the most common mistakes I have witnessed in my eight years as an operational analyst.

Myth 1: Six Sigma is all about the normal distribution

Many green and black belt candidates and graduates don’t seem to fully understand the need to determine the shape of the distribution of the data they are analyzing. The misconceptions they have and misapply have become so prominent that even managers and directors who have never had Six Sigma training seem to have developed the same feelings through some form of mathematical osmosis.

Ask any high-level director, whether they have been trained in Six Sigma concepts or not, and the common response you hear is, “Oh yeah, the normal distribution, three standard deviations from the mean, I know all about Six Sigma.” What exactly are they saying?

The point is exacerbated even further by the responses I receive from many of the students I have mentored. When determining the normality of any data set we are analyzing, a common response goes as follows:

Mentor: “According to the Anderson-Darling normality test, the data set we are working with does follow a normal distribution.”

Student: “Oh, thank goodness.”

The students make it seem that if the data set does not conform to normality, then there is a massive problem with their project. The fact is that determining normality is important because it will act as a roadmap for further analysis down the road. Some comparative hypothesis tests are sensitive to normality, while others are not. There is nothing inherently good or bad if a data set is not normally distributed. When working with data sets that are skewed or non-normally distributed, there are a slew of additional metrics (e.g., median, inter-quartile range) and advanced analysis techniques (e.g., nonparametric) that are at our disposal. We need to determine normality so that we apply the appropriate statistical tests and concepts for the duration of the project, yet many practitioners view the subject of normality as an all-inclusive adjective; normally distributed data = good.

Myth 2: You have two processes, A and B, and your null hypotheses (Ho) is that these processes are equal in terms of efficiency (Ho: A = B). If after running the appropriate statistical tests for equality, you determine that you cannot reject process A for process B, then this proves that process A is better than process B.

This concept emerges time and time again. Somehow the idea of failing to reject one process for another gets translated into the original process is clearly superior to the new proposed process. The truth of the matter is you really don’t know, and can’t say, if one process is “better” than the other. All you can say for certain is that you are 95% confident (assuming an alpha of 0.05) that you should not reject process A for process B.

The good news is that there are steps you can take to obtain that level of clarity. Part of the problem stems from the training, which has become outdated. Ten years ago, it was not uncommon to hear expressions like, “When p is low, the null must go.” Or, “If p is high, the null will fly.” While these phrases were meant as a teaching guide to help assist new Six Sigma practitioners, they may do more harm than good if used incorrectly. While it is still true that if the p-value is low you can reject Ho, a more appropriate phrase for the second aspect would be, “If p is not low, then you don’t know about Ho.”

This leads to the third step of hypothesis test conclusions: “If p is not low, but your power of the test is high, then you can be confident that Ho is at least nearly true.” This step about the power of a test is largely unexplored by many Six Sigma practitioners. Once the hypothesis test is completed, they either reject or fail to reject Ho based solely on their p-value. Most Six Sigma practitioners can identify alpha error, but do not seem as concerned about committing a type 2 beta error. This leads us to another common misconception practiced by many…

Myth 3: A type 1 error (alpha) is worse than a type 2 (beta) error.

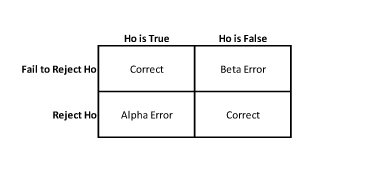
When the subject of hypothesis testing is initially taught, most instructors define what each type of error is and provide a simple four-fold table to display the concept.

Alpha Error (type I): Rejecting Ho when it is true.

Beta Error (type II): Failing to reject Ho when it is false.

This is commonly followed by a question: Which error is worse? The answer generally provided is that an alpha error is typically worse than a beta error, because with an alpha error, you are suggesting moving to a new process when no change is required, but with a beta error, you should reject Ho and move to a new process but fail to do so, so the process remains roughly the same.

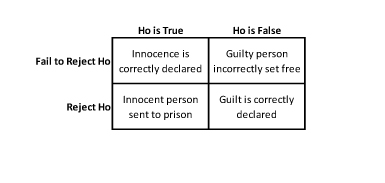
This concept is further cemented into the student’s minds with an example of a person on trial for an extreme crime.

Ho = Innocence

Ha = Guilt

The conclusion is that sentencing an innocent person to prison (alpha) is much worse than setting a guilty person free (beta). Although both mistakes are costly, most people would tend to agree that sending an innocent person to jail is, in fact, worse than setting a guilty person free.

What is getting lost in translation through all of this is the subject of context. Most Six Sigma students are going to use the skills they learn in the context of business. In business, whether we cost a company $3 million by suggesting an alternative process when there is nothing wrong with the current process or we fail to realize $3 million in gains when we should switch to a new process but fail to do so, the end result is the same. The company failed to capture $3 million in additional revenue. Yet somehow, the idea that an alpha error is inherently worse than a beta error has become standardized among many Six Sigma students.

In summation, there are countless other examples of Six Sigma concepts being misunderstood and used incorrectly. The three examples here appear to be some of the more common mistakes being perpetuated. When this occurs, companies are, in essence, paying for training that will lead to more errors and greater confusion, rather than a new management philosophy that will lead to greater returns and fewer defects. However, with updated training techniques and an increasing number of resources, many practitioners of Six Sigma can hopefully avoid these pitfalls and help their respective companies truly achieve greater efficiencies.